Quando estudamos a potenciação, vimos que 23 é igual a 2 . 2 . 2 que é igual a 8. Partimos do número 2 e através de uma multiplicação de 3 fatores iguais a 2, chegamos ao número 8. Agora temos o caminho inverso, araiz cúbica de oito é a operação que nos aponta qual é número que elevado a 3 é igual a 8, ou seja, é a operação inversa da potenciação.
Raízes de Radicando Real com Índice Não Nulo
A raiz enésima de a é igual a b, se e somente se b elevado a enésima potência for igual a a:
Não Existe a Raiz de um Radicando Negativo e Índice Par
Por quê?
Vamos tomar como exemplo a raiz quadrada de menos 16 expressa por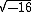 
. Segundo a definição temos:
Qual é o valor numérico que b deve assumir para que multiplicado por ele mesmo seja igual a -16?
Como sabemos na multiplicação de números reais ao multiplicarmos dois números, diferentes de zero, com o mesmo sinal, o resultado sempre será positivo, então não existe um número no conjunto dos números reais que multiplicado por ele mesmo dará um valor negativo, pois o sinal é o mesmo em ambos os fatores da multiplicação.
A Raiz de um Radicando Negativo e Índice Ímpar é Negativa
Em uma multiplicação se todos os sinais forem positivos, obviamente o produto final também será positivo, já se tivermos fatores negativos, se estes forem em quantidade par o resultado será positivo, se forem em quantidade ímpar o resultado será negativo. É evidente que nenhum dos fatores pode ser igual a zero. Então a raiz enésima de a, um número real negativo será negativa se o índice for ímpar. Se for par como vimos acima, não existirá.
Vamos analisar a raiz quinta de menos 32 que se expressa como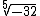 
:
Como o expoente de b é ímpar, ou seja, o número de fatores que representa a potência é impar, para que o resultado seja -32, é preciso que b seja negativo. Então a raiz de um número negativo e índice ímpar sempre será um número negativo.
Neste exemplo -2 é o número negativo que elevado a 5 resulta em -32, logo:
Note que na potência colocamos o -2 entre parênteses, pois se não o fizéssemos, apenas o 2 estaria elevado à quinta potência. Como o expoente é ímpar, não faria diferença no resultado se não os tivéssemos utilizado, mas isto seria imprescindível se o expoente fosse um número par, para que não houvesse erro de sinal no resultado da potenciação.
A Raiz de um Radicando Positivo também é Positiva
Não importa se o índice é par ou impar, em não sendo nulo, a raiz de um radicando positivo também será positiva.
Vamos analisar a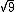 
, que se lê raiz quadrada de nove:
Logo 3 é o número que elevado ao quadrado dá 9.
Mas você pode também se perguntar:
E se for -3? Se elevarmos -3 ao quadrado também iremos obter nove!
Correto, mas lembra-se da definição da raiz para um radicando positivo?
Tanto o radicando quanto a raiz devem ser positivos, é por isto que não podemos considerar o -3.
A Raiz de um Radicando Nulo também é Nula
Isto é verdade desde que o índice não seja nulo também.
Exemplo:
Propriedades da Radiciação
As propriedades que vamos estudar agora são consideradas no conjunto dos números reais positivos ou nulos, podendo não se verificar caso o radicando seja negativo, pois como sabemos, não existe raiz real de um número negativo.
A Raiz de uma Potência é uma Potência com Expoente Fracionário
Assim como de uma potenciação podemos chegar a uma radiciação, desta podemos chegar a uma potenciação:
Exemplo:
Já que n não pode ser zero, a partir desta propriedade concluímos que não existe raiz de índice zero. Se n fosse zero, o denominador da fração do expoente seria zero, que sabemos não ser permitido.
Mudança de Índice pela sua Multiplicação/Divisão e do Expoente do Radicando por um Mesmo número Não Nulo
Se multiplicarmos ou dividirmos tanto o índice do radical, quanto o expoente do radicando por um mesmo número diferente de zero, o valor do radical continuará o mesmo:
Exemplos:
Raiz de uma Potência
A raiz n de uma potência de a elevado a m, é a potência m da raiz n de a:
Exemplo:
Produto de Radicais de Mesmo Índice
O produto de dois radicais de mesmo índice é igual à raiz deste índice do produto dos dois radicandos:
Exemplo:
Vamos verificar:
Divisão de Radicais de Mesmo Índice
O quociente de dois radicais de mesmo índice é igual a raiz deste índice do quociente dos dois radicandos:
Exemplo:
Verificando:
Simplificação de Radicais Através da Fatoração
Podemos simplificar e em alguns casos até mesmo eliminar radicais, através da decomposição do radicando em fatores primos. O raciocínio é simples, decompomos o radicando em fatores primos por fatoração e depois simplificamos os expoentes que são divisíveis pelo índice do radicando.
Vamos simplificar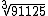 
decompondo 91125 em fatores primos:
Como 91125 = 36 . 53 podemos dizer que:
Repare que tanto o expoente do fator 36, quanto o expoente do fator 53 são múltiplos do índice do radicando que é igual a 3. Vamos então simplificá-los:
Perceba que através da fatoração de 91125 e da simplificação dos expoentes dos fatores pelo índice do radicando, extraímos a sua raiz cúbica eliminando assim o radical.
Vejamos agora o caso do radical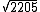 
:
Logo 2205 = 32 . 5 . 72, então:
Como os expoentes dos fatores 32 e 72 são divisíveis pelo índice 2, vamos simplificá-los retirando-os assim do radical:
Neste caso o expoente do fator 5 não é divisível pelo índice 2 do radicando, por isto após a simplificação não conseguimos eliminar o radical.
Agora vamos analisar o número 
:
Note que 729 = 36, então:
Neste caso o expoente de 36 não é divisível pelo índice 5, mas é maior, então podemos escrever:
Repare que agora o expoente do fator 35 é divisível pelo índice 5, podemos então retirá-lo do radical:
Agora vamos pensar um pouco. Após a fatoração tínhamos o radical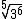 
. O expoente 6 não é divisível por 5, pois ao realizarmos a divisão, obtemos um quociente de 1 e um resto também de 1. Pois bem, o 1 do quociente será o expoente da base 3 ao sair o radical. A parte que ainda ficou no radical terá como expoente o 1 do resto. Vamos a alguns exemplos para melhor entendermos a questão:
Simplifique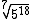 
.
Dividindo 18 por 7 obtemos um quociente de 2 é um resto de 4, logo fora do radical a base 5 terá o expoente 2do quociente e a base dentro do radical terá o expoente 4 que é o resto da divisão:
Logo:
Outro exemplo, simplifique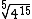 
.
A divisão de 15 por 5 resulta em quociente 3 e resto 0, pois a divisão é exata, mas não há problema. Seguindo as explicações temos:
Veja que quando o é resto for zero podemos eliminar o radical, já que o radicando sempre será igual a 1, pois todo número natural não nulo elevado a zero é igual a um:
Nos casos em que os expoentes de todos os fatores forem menores que o índice do radical como, por exemplo, em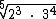
, a simplificação não poderá ser realizada.
=
o 2/3 está elevado a primeira dentro dos parênteses. Ficará assim:
fim! Há outro jeito de fazer isso veja:
=cuidado com o sinal negativo! Existem várias maneiras de resolver isso aqui, vejamos:
=
repare que o sinal de negativo está fora dos parênteses, logo, ficou fora da potenciação ok! Lembre-se há outras maneiras de resolver esses exercícios.
enfim, 
=224 , pois os expoentes estão multiplicando, 3.2.4=24, por iss
=24 pois fazendo as operações com os expoentes 8-4=4
= 5-5 pois fazendo as operações com os expoentes 2-7=-5
= 310 pois fazendo as operações com os expoentes 3-(-7)=+10 veja a regra de sinal, menos com menos virou +
=6-4 pois fazendo as operações com os expoentes -9-(-5)= -4 veja a regra de sinal, menos com menos virou + e como o nove é maior, ficou o sinal negativo
23.52 = 8.25= 200 repare que só foi invertido o 5-2, pois o 23 o expoente 3 já estava positivo, e não foi invertido, só é pra inverter quando o expoente estiver negativo!
só inverti o 6 elevado a dois negativo!
=
=
=36
fazendo a continha 